pytorch基础操作

前言：

​ 此篇主要涉及pytorch的入门内容，主要是张量的基础操作以及使用pytorch进行反向传播，最后还简要介绍了pytorch的一系列常用的基础组件，以便对后续更深层次的学习任务奠定基础。

一、创建张量

1.1 简单张量

根据已有数据创建张量,torch.tensor默认数字类型是float32

def test0():
    # 创建标量
    data = torch.tensor(10)
    print(data)

    # 使用numpy数组创建张量
    data = np.random.randn(2,3)
    data = torch.tensor(data)
    print(data)

    # 使用列表创建多维张量
    data = [[[i for i in range(10)],[j for j in range(10,20)]]]
    data = torch.tensor(data)
    print(data)
test0()

tensor(10)
tensor([[ 0.5558, 0.0213, 0.4975],
[ 0.1977, 2.0550, -0.3598]], dtype=torch.float64)
tensor([[[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14, 15, 16, 17, 18, 19]]])

创建指定形状张量

def test1():
    # 创建两行三列张量
    data = torch.Tensor(2,3)
    print(data)
    # 创建指定值张量
    data = torch.Tensor([2,3])
    print(data)

test1()

tensor([[1., 1., 1.],
[1., 1., 1.]])
tensor([2., 3.])

创建指定类型张量,传递数据如果不匹配会发生类型转换

def test2():
    # 创建int类型张量
    data = torch.IntTensor(2,3)
    print(data)
    
    # 创建float类型张量
    data = torch.FloatTensor(2,3)
    print(data)


test2()

tensor([[772014944, 1301, 0],
[ 0, 0, 0]], dtype=torch.int32)
tensor([[0., 0., 0.],
[0., 0., 0.]])

1.2 线性张量和随机张量

创建线性张量

def test3():
    # 创建指定步长张量
    # arange(start,end,步长)
    data = torch.arange(0,10,2)
    data = torch.Tensor(data)
    print(data)
    # 指定区间指定元素个数
    # linspace(start,end,元素个数)
    data = torch.linspace(0,10,100)
    data = torch.Tensor(data)
    print(data)
test3()

tensor([0, 2, 4, 6, 8])
tensor([ 0.0000, 0.1010, 0.2020, 0.3030, 0.4040, 0.5051, 0.6061, 0.7071,
0.8081, 0.9091, 1.0101, 1.1111, 1.2121, 1.3131, 1.4141, 1.5152,
1.6162, 1.7172, 1.8182, 1.9192, 2.0202, 2.1212, 2.2222, 2.3232,
2.4242, 2.5253, 2.6263, 2.7273, 2.8283, 2.9293, 3.0303, 3.1313,
3.2323, 3.3333, 3.4343, 3.5354, 3.6364, 3.7374, 3.8384, 3.9394,
4.0404, 4.1414, 4.2424, 4.3434, 4.4444, 4.5455, 4.6465, 4.7475,
4.8485, 4.9495, 5.0505, 5.1515, 5.2525, 5.3535, 5.4545, 5.5556,
5.6566, 5.7576, 5.8586, 5.9596, 6.0606, 6.1616, 6.2626, 6.3636,
6.4646, 6.5657, 6.6667, 6.7677, 6.8687, 6.9697, 7.0707, 7.1717,
7.2727, 7.3737, 7.4747, 7.5758, 7.6768, 7.7778, 7.8788, 7.9798,
8.0808, 8.1818, 8.2828, 8.3838, 8.4848, 8.5859, 8.6869, 8.7879,
8.8889, 8.9899, 9.0909, 9.1919, 9.2929, 9.3939, 9.4949, 9.5960,
9.6970, 9.7980, 9.8990, 10.0000])

创建随机张量

def test4():
    # 随机种子
    torch.random.manual_seed(42)
    data = torch.randn(2,3)
    data = torch.Tensor(data)
    print(data)
test4()

tensor([[ 0.3367, 0.1288, 0.2345],
[ 0.2303, -1.1229, -0.1863]])

1.3 指定值张量

def test5():
    # 创建全为零的张量
    data = torch.zeros(2,3)
    print(data)
    # 根据其他张量的形状创建全0张量
    data1 = torch.zeros_like(data)
    print(data1)
    # 创建全为一的张量,ones_like同理
    data = torch.ones(2,3)
    print(data)
    # 创建指定值张量,torch.fill(形状，填充值),full_like同理
    data = torch.full([2,3],6)
    print(data)
test5()

tensor([[0., 0., 0.],
[0., 0., 0.]])
tensor([[0., 0., 0.],
[0., 0., 0.]])
tensor([[1., 1., 1.],
[1., 1., 1.]])
tensor([[6, 6, 6],
[6, 6, 6]])

1.4 张量元素类型转换

def test6():
    # type函数转换
    data = torch.full([2,3],6)
    print("转换前",data.dtype)
    # 会返回一个新类型的变量而不是直接修改原张量
    data1 = data.type(torch.FloatTensor)
    print("转换后",data1.dtype)

    # 使用具体类型函数转换
    data2 = data.float()
    print("转换后",data2.dtype)
test6()

转换前 torch.int64
转换后 torch.float32
转换后 torch.float32

二、数值计算

2.1 张量的基本运算

加减乘除相反数

def test0():
    torch.random.manual_seed(40)
    # torch.randint(start,end,形状)
    data = torch.randint(0,10,[2,3])
    print(data)
    # 计算完成后会产生一个新的张量,满足计算广播机制
    # 加法
    tensor = torch.randint(0,10,[2,1])
    print(tensor)
    data_add = data.add(tensor)
    print("data_add",data_add)
    # 减法
    data_sub = data.sub(tensor)
    print("data_sub",data_sub)
    # 乘法
    data_mul = data.mul(data_sub)
    print("data_mul",data_mul)
    # 除法
    data_div = data.div(tensor)
    print("data_div",data_div)
    # 取相反数
    data_neg = data.neg()
    print("data_neg",data_neg)
test0()

tensor([[8, 3, 5],
[7, 2, 4]])
tensor([[6],
[3]])
data_add tensor([[14, 9, 11],
[10, 5, 7]])
data_sub tensor([[ 2, -3, -1],
[ 4, -1, 1]])
data_mul tensor([[16, -9, -5],
[28, -2, 4]])
data_div tensor([[1.3333, 0.5000, 0.8333],
[2.3333, 0.6667, 1.3333]])
data_neg tensor([[-8, -3, -5],

def test2():
    # 使用mul函数
    data1 = torch.tensor([[1,2],[3,4]])
    data2 = torch.tensor([[5,6],[7,8]])
    data = data1.mul(data2)
    print(data)
    # 使用*
    data = data1*data2
    print(data)
test2()

 [-7, -2, -4]])

修改原数据的运算，不需要额外变量来接收运算结果

直接在原有运算方法名后面加下划线

def test1():
    torch.random.manual_seed(40)
    data = torch.randint(0,10,[2,3])
    print(data)
    tensor = torch.randint(0,10,[2,1])
    print(tensor)
    data.add_(tensor)
    print("result",data)
test1()

tensor([[8, 3, 5],
[7, 2, 4]])
tensor([[6],
[3]])
result tensor([[14, 9, 11],
[10, 5, 7]])

2.2 阿达玛积

阿达玛积:张量对应位置元素相乘

def test2():
    # 使用mul函数
    data1 = torch.tensor([[1,2],[3,4]])
    data2 = torch.tensor([[5,6],[7,8]])
    data = data1.mul(data2)
    print(data)
    # 使用*
    data = data1*data2
    print(data)
test2()

tensor([[ 5, 12],
[21, 32]])
tensor([[ 5, 12],
[21, 32]])

2.3 点积运算

def test3():
    # 使用@运算符直接对两个二维矩阵进行计算
    data1 = torch.tensor([[1,2],[3,4],[5,6]])
    data2 = torch.tensor([[5,6],[7,8]])
    data = data1@data2
    print("@",data)

    # 使用mm函数，要求输入张量形状都是二维的
    data1 = torch.tensor([[1,2],[3,4],[5,6]])
    data2 = torch.tensor([[5,6],[7,8]])
    data = torch.mm(data1,data2)
    print("mm",data)

    # 使用bmm函数运算，要求输入数据必须是三维
    torch.random.manual_seed(40)
    # torch.randn(批次，行，列)
    data1 = torch.randn(3,4,5)
    print(data1)
    data2 = torch.randn(3,5,8)
    data = torch.bmm(data1,data2)
    print("bmm",data.shape)

    # 使用matmul函数
    data1 = torch.randn(4,5)
    data2 = torch.randn(5,6)
    data = torch.matmul(data1,data2)
    print("matmul1",data.shape)

    data1 = torch.randn(3,4,5)
    data2 = torch.randn(3,5,8)
    data = torch.matmul(data1,data2)
    print("matmul2",data.shape)
test3()

@ tensor([[19, 22],
[43, 50],
[67, 78]])
mm tensor([[19, 22],
[43, 50],
[67, 78]])
tensor([[[-0.2367, 1.8109, 0.1966, -0.7150, 0.1041],
[ 0.8893, -0.4212, -0.5279, 0.9281, 0.8614],
[-0.5856, 1.4157, -1.9983, -0.7397, -1.1917],
[ 0.0635, -1.3966, 0.4813, -1.2866, 0.1643]],

​ [[ 0.4827, 0.4881, -1.8173, 1.0127, 1.3802],
​ [ 0.0903, 0.7811, 0.0891, 0.1531, -0.2344],
​ [ 0.0868, -1.5610, -0.5121, -0.9283, 1.0775],
​ [ 0.1593, -1.8646, 0.5430, 1.4348, 1.1829]],

​ [[-0.3522, 0.9055, -0.1248, -0.1938, -0.3097],
​ [-1.4255, 1.2274, -1.7690, -1.6122, 0.4332],
​ [ 1.6599, 1.6113, 0.1054, 0.1470, 1.1172],
​ [-0.2970, -0.1661, -0.8077, -0.0500, 0.1276]]])
bmm torch.Size([3, 4, 8])
matmul1 torch.Size([4, 6])
matmul2 torch.Size([3, 4, 8])

三、 数值转换

3.1 tensor张量转numpy数组

转换后的两个数据共享内存地址，可以使用copy()来区分开来

def test0():
    data_tensor = torch.tensor([1,2,3])
    # 将张量转换为numpy数组
    data_np = data_tensor.numpy()
    print(data_tensor,type(data_tensor))
    print(data_np,type(data_np))

    # 此时两个数据共享内存
    data_tensor[0] = 2
    print("修改tensor后")
    print(data_tensor)
    print(data_np)
    
    data_np[0] = 3
    print("修改numpy后")
    print(data_tensor)
    print(data_np)

    # 使用copy函数实现不共享内存
    data_tensor = torch.tensor([1,2,3])
    data_np = data_tensor.numpy().copy()
    data_tensor[0] = 2
    print("修改copy的tensor后")
    print(data_tensor)
    print(data_np)

    data_np[0] = 3
    print("修改copy的numpy后")
    print(data_tensor)
    print(data_np)

test0()

tensor([1, 2, 3]) <class ‘torch.Tensor’>
[1 2 3] <class ‘numpy.ndarray’>
修改tensor后
tensor([2, 2, 3])
[2 2 3]
修改numpy后
tensor([3, 2, 3])
[3 2 3]
修改copy的tensor后
tensor([2, 2, 3])
[1 2 3]
修改copy的numpy后
tensor([2, 2, 3])
[3 2 3]

3.2 numpy数组转tensor张量

def test1():
  data_numpy = np.array([2,3,4])
  # from_numpy函数,默认共享内存
  data_tensor1 = torch.from_numpy(data_numpy)
  # 设置不共享地址
  data_tensor_copy = torch.from_numpy(data_numpy.copy())
  print(data_tensor1)
  # 使用tensor，默认不共享内存
  data_tensor2 = torch.tensor(data_numpy)
  print(data_tensor2)


test1()

tensor([2, 3, 4])
tensor([2, 3, 4])

3.3 标量张量和数字的转换

使用item()提取数字，只适用于张量中只有一个元素的情况

def test2():
    data1 = torch.tensor(0)
    data2 = torch.tensor([10])
    data3 = torch.tensor([[20]])
    print(data1.shape,data2.shape,data3.shape)

    num1 = data1.item()
    num2 = data2.item()
    num3 = data3.item()
    print(num1,num2,num3)
test2()

torch.Size([]) torch.Size([1]) torch.Size([1, 1])
0 10 20

四、拼接操作

4.1 torch.cat（连接操作）

• 功能：沿指定维度连接多个张量，输入张量的形状（除拼接维度外）必须完全相同。
• 不新增维度，仅扩展现有维度的大小。
• 适用于需要合并数据但无需新增维度的场景（如拼接多个特征向量）。

import torch
x = torch.randn(2, 3)
y = torch.randn(2, 3)
# 沿维度0拼接（行方向）
z_cat = torch.cat([x, y], dim=0)  # 输出形状：(4, 3)

4.2 torch.stack（堆叠操作）

• 功能：在新创建的维度上堆叠多个张量，所有输入张量的形状必须完全一致。
• 新增一个维度，堆叠后的张量比输入张量多一维。
• 适用于需要创建批次维度或组合多个张量的场景（如创建图像批次）。

# 相同输入张量x和y
z_stack = torch.stack([x, y], dim=0)  # 输出形状：(2, 2, 3)

关键差异总结

• 维度变化：cat不新增维度，stack会新增一个维度。
• 输入要求：cat允许拼接维度的大小不同（其他维度相同），stack要求所有维度完全一致。
• 典型用途：cat用于合并数据序列，stack用于构建批次或组合张量。

五、索引操作

5.1 简单行列索引

def test0():
    torch.random.manual_seed(42)
    data = torch.randint(0,10,(4,5))
    print(data)

    # 获得某行某列元素
    print(data[0])

    print(data[0,1])
    print(data[0][1])
    
    # 左行右列，左闭右开
    print(data[:3,2:3])
    print(data[:3][2:3])

test0()

tensor([[2, 7, 6, 4, 6],
[5, 0, 4, 0, 3],
[8, 4, 0, 4, 1],
[2, 5, 5, 7, 6]])
tensor([2, 7, 6, 4, 6])
tensor(7)
tensor(7)
tensor([[6],
[4],
[0]])
tensor(7)

5.2 布尔索引

def test1():
    torch.random.manual_seed(42)
    data = torch.randint(0,100,(4,5))
    print(data)

    # 获取所有大于30的元素
    print(data[data>30])

    # 获取第二列有元素大于20的行
    print(data[data[:,1]>=20])

test1()

tensor([[42, 67, 76, 14, 26],
[35, 20, 24, 50, 13],
[78, 14, 10, 54, 31],
[72, 15, 95, 67, 6]])
tensor([42, 67, 76, 35, 50, 78, 54, 31, 72, 95, 67])
tensor([[42, 67, 76, 14, 26],
[35, 20, 24, 50, 13]])

5.3 多维索引

def test2():
    torch.random.manual_seed(42)
    data = torch.randint(0,100,(3,4,5))
    print(data)

    print(data[0,:,:])
    print(data[:,0,:])
    print(data[:,:,0])

test2()

tensor([[[42, 67, 76, 14, 26],
[35, 20, 24, 50, 13],
[78, 14, 10, 54, 31],
[72, 15, 95, 67, 6]],

​ [[49, 76, 73, 11, 99],
​ [13, 41, 69, 87, 19],
​ [72, 80, 75, 29, 33],
​ [64, 39, 76, 32, 10]],

​ [[86, 22, 77, 19, 7],
​ [23, 43, 94, 93, 77],
​ [70, 9, 70, 39, 86],
​ [99, 15, 84, 78, 8]]])
tensor([[42, 67, 76, 14, 26],
​ [35, 20, 24, 50, 13],
​ [78, 14, 10, 54, 31],
​ [72, 15, 95, 67, 6]])
tensor([[42, 67, 76, 14, 26],
​ [49, 76, 73, 11, 99],
​ [86, 22, 77, 19, 7]])
tensor([[42, 35, 78, 72],
​ [49, 13, 72, 64],
​ [86, 23, 70, 99]])

六、形状操作

6.1 reshape()函数

def test0():
  torch.random.manual_seed(42)
  data = torch.randint(0,10,[4,5])
  print(data.shape)

  # 修改张量形状
  new_data = torch.reshape(data,[2,10])
  print(new_data.shape)

  # 使用-1自动匹配形状
  new_data = torch.reshape(data,[-1,20])
  print(new_data.shape)


test0()

torch.Size([4, 5])
torch.Size([2, 10])
torch.Size([1, 20])

6.2 transpose()函数和permute()函数

transpose只是简单进行维度交换,一次只能交换两个维度,permute函数在transpose基础上可以一次交换多个维度

def test1():
    torch.random.manual_seed(42)
    data = torch.randint(0,10,[3,4,5])
    print(data.shape)
    print(data)
    print("-"*50)

    # reshape重新计算形状
    data_reshape = torch.reshape(data,[4,3,5])
    print(data_reshape.shape)
    print(data_reshape)
    print("-"*50)

    data_transpose = torch.transpose(data,0,1)
    print(data_transpose.shape)
    print(data_transpose)
    print("-"*50)

    data_permute = torch.permute(data,(2,0,1))
    print(data_permute.shape)
    print(data_permute)

test1()

6.3 view()函数和contigous()函数

def test1():
    # view函数的使用
    data = torch.tensor([[10,20,30],[40,50,60]])
    data_view = data.view(3,2)
    print(data_view.shape)

    # 使用is_contigous判断张量是否是连续的内存空间
    print(data.is_contiguous())

    # 如果不是连续的内存空间，不可以使用view来更改维度
    data_transpose = torch.transpose(data,0,1)
    print(data_transpose.is_contiguous())# 非连续
    # print(data_transpose.view(2,3))# 非连续地址，报错

    # 使用contiguous()将非连续内存改为连续内存
    print(data_transpose.contiguous().view(2,3))

test1()

torch.Size([3, 2])
True
False
tensor([[10, 40, 20],
[50, 30, 60]])

6.4 squeeze()函数和unsqueeze()函数

def test2():
    # squeeze函数降维，去除数据中的1维度
    data = torch.randint(1,10,[1,3,1,5])
    print(data.shape)
    print(data)
    data_squ = data.squeeze()
    print(data_squ.shape)
    print(data_squ)

    # 制定去除第二个1的维度
    data_squ_1 = data.squeeze(2)
    print(data_squ_1.shape)
    print(data_squ_1)

    print("-"*50)

    # unsqueeze函数升维
    data = torch.randint(1,10,[3,4,5])
    print(data.shape)
    # 参数表示升维的位置
    data_unsqu = data.unsqueeze(-1)
    print(data_unsqu.shape)
    

test2()

torch.Size([1, 3, 1, 5])
tensor([[[[3, 4, 3, 8, 1]],

​ [[6, 7, 2, 8, 8]],

​ [[9, 1, 8, 8, 8]]]])
torch.Size([3, 5])
tensor([[3, 4, 3, 8, 1],
​ [6, 7, 2, 8, 8],
​ [9, 1, 8, 8, 8]])
torch.Size([1, 3, 5])
tensor([[[3, 4, 3, 8, 1],
​ [6, 7, 2, 8, 8],
​ [9, 1, 8, 8, 8]]])
-————————————————-
torch.Size([3, 4, 5])
torch.Size([3, 4, 5, 1])

七、运算函数

运算规则和numpy类似

def test0():
    torch.random.manual_seed(42)
    data1 = torch.randint(0,5,[2,3],dtype=torch.float64)
    print(data1)
    data2 = torch.randint(5,10,[2,3],dtype=torch.float64)

    # 均值,默认对所有数据计算均值
    print(data1.mean())
    # 按照指定维度
    print(data1.mean(dim=1))# 行
    print(data1.mean(dim=0))# 列

    # 求和sum()
    # 平方pow()
    # 平方根sqrt()
    # 指数幂exp()
    # 对数log2()

test0()

tensor([[2., 2., 1.],
[4., 1., 0.]], dtype=torch.float64)
tensor(1.6667, dtype=torch.float64)
tensor([1.6667, 1.6667], dtype=torch.float64)
tensor([3.0000, 1.5000, 0.5000], dtype=torch.float64)

八、反向传播

8.1 梯度基本计算

8.1.1 标量梯度计算

对于需要求导的张量需要设置参数为True,并且类型指定为小数

def test0():
    x = torch.tensor(10,requires_grad=True,dtype=torch.float64)
    f = x**2+20

    # backward进行自动微分,2*x
    f.backward()

    # grad访问梯度
    print(x.grad)

test0()

tensor(20., dtype=torch.float64)

8.1.2 向量梯度计算

上面f计算出来的是一个向量，不能直接求梯度，梯度必须是在标量基础上的

用均值或求和来表示f使f变成标量

def test1():
    x = torch.tensor([10,20,30,40],requires_grad=True,dtype=torch.float64)

    f = x**2+20
    print("f",f)

    f_mean = f.mean() # f_mean = f/4

    f_mean.backward()

    # grad访问梯度
    print(x.grad)

test1()

f tensor([ 120., 420., 920., 1620.], dtype=torch.float64,grad_fn=)
tensor([ 5., 10., 15., 20.], dtype=torch.float64)

8.1.3 多标量梯度计算

多标量其实大差不差，只是最后要分开访问变量的梯度值就行了

def test2():
    x1 = torch.tensor(10,requires_grad=True,dtype=torch.float64)
    x2 = torch.tensor(20,requires_grad=True,dtype=torch.float64)
    f = x1**2+x2**2+2*x1
    print("f",f)

    f.backward()

    # grad分别访问x1,x2梯度
    print(x1.grad)
    print(x2.grad)

test2()

f tensor(520., dtype=torch.float64, grad_fn=)
tensor(22., dtype=torch.float64)
tensor(40., dtype=torch.float64)

8.1.4 多向量梯度计算

def test3():
    x1 = torch.tensor([10,20,30,40],requires_grad=True,dtype=torch.float64)
    x2 = torch.tensor([40,50,60,70],requires_grad=True,dtype=torch.float64)
    f = x1**2+x2**2+2*x1
    print("f",f)

    # 转为标量
    f_mean = f.sum()

    f_mean.backward()

    # grad分别访问x1,x2梯度
    print(x1.grad)
    print(x2.grad)

test3()

f tensor([1720., 2940., 4560., 6580.], dtype=torch.float64,
grad_fn=)
tensor([22., 42., 62., 82.], dtype=torch.float64)
tensor([ 80., 100., 120., 140.], dtype=torch.float64)

8.2 控制梯度计算

8.2.1 控制梯度计算

可以通过控制梯度计算，来设定忽略某个变量的梯度，设定后计算梯度将自动跳过

第一种方式：

def test4():
    x = torch.tensor(10,requires_grad=True,dtype=torch.float64)
    # 此时可以调用backward计算f的梯度
    print(x.requires_grad)


    with torch.no_grad():
        f = x**2
    print(f.requires_grad)


test4()

True
False

第二种方式：

@torch.no_grad()
def my_func(x):
    return x**2
f = my_func(x)
print(f.requires_grad)

False

第三种方式：全局禁用梯度

由于 f 是在禁用梯度计算的上下文中生成的，因此会抛出错误

torch.set_grad_enabled(False)
f = x**2
print(f.requires_grad)

f.backward()

# grad访问梯度
print(x.grad)

8.2.2 累计梯度和梯度清零

通过循环重复对x进行计算会将历史梯度值累加到x.grad属性中,相当于通过循环多次求导

def test5():
    x = torch.tensor([10,20,30,40],requires_grad=True,dtype=torch.float32)

    for _ in range(3):
        f1 = x**2+20
        # 将向量转换为标量
        f2 = f1.mean()
        # 自动微分
        f2.backward()
        print(x.grad)
test5()  

tensor([ 5., 10., 15., 20.])
tensor([10., 20., 30., 40.])
tensor([15., 30., 45., 60.])

但是在实际的梯度下降求解最优参数中，我们不希望这样的累加行为来影响梯度求解的结果，而是每次循环有不一样的数据来对损失函数进行优化，因此每次循环要进行梯度清零

def test6():
    x = torch.tensor([10,20,30,40],requires_grad=True,dtype=torch.float32)

    for _ in range(3):
        f1 = x**2+20
        # 将向量转换为标量
        f2 = f1.mean()

        # 梯度清零
        if x.grad is not None:
            x.grad.data.zero_()
            
        # 自动微分
        f2.backward()
        print(x.grad)
test6() 

在PyTorch中，梯度是累加的。这意味着每次调用 .backward() 时，计算得到的梯度会被累加到现有的梯度上，而不是替换它。如果不进行梯度清零，历史梯度会不断累积，导致梯度值变得非常大，这会影响模型的训练效果。

8.2.3 梯度下降优化算法案例

在梯度清零的基础上，我们需要更新每次循环后的参数

def test7():
    # 初始化一个x和theta
    x = torch.tensor(10,requires_grad=True,dtype=torch.float64)
    theta = 0.01
    for i in range(1000):
        # 前向传播
        y = x**3

        # 梯度清零
        if x.grad is not None:
            x.grad.data.zero_()
        
        # 自动微分
        y.backward()

        # 更新参数
        x.data = x.data-theta*x.grad

        # 打印x值
        print(x.data)

test7()

8.3 梯度计算注意

detach() 方法用于将张量从计算图中分离出来，返回一个新的张量，该张量与原始张量共享数据，但不会参与梯度计算。它的主要用途包括防止梯度传播、节省内存和优化模型推理。

8.3.1 简单演示

def test8():
    x = torch.tensor([10,20],requires_grad=True,dtype=torch.float64)
    # 演示上述错误
    # print(x.numpy())
    # 演示正确操作
    print(x.detach().numpy())
test8()

8.3.2 解决方案：detach()数据共享

解释：

def test9():
    # 演示正确操作
    x1 = torch.tensor([10,20],requires_grad=True,dtype=torch.float64)
    x2 = x1.detach()
    print(id(x1.data),id(x2.data))
    
    x2[0] = 100
    print(x1)
    
test9()

1607428373376 1607428373376
tensor([100., 20.], dtype=torch.float64, requires_grad=True)

九、基础组件

import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.datasets import make_regression
import matplotlib.pyplot as plt
from torch.utils.data import Dataset,DataLoader,TensorDataset

9.1 基础组件的用法

9.1.1 损失函数

def test0():

  # 初始化平方损失函数对象
  criterion = nn.MSELoss()

  # 该对象可以当做函数来使用
  torch.random.manual_seed(42)
  y_pred = torch.randn(3,5,requires_grad=True)
  y_true = torch.randn(3,5,requires_grad=True)

  # 计算损失
  loss = criterion(y_pred,y_true)
  print(loss)  

test0()

tensor(1.0192, grad_fn=)

9.1.2 线性假设函数

def test1():
    # 输入数据特征为10，输出数据特征为5
    model = nn.Linear(in_features=10,out_features=5)

    # 构建4行10列输入数据
    input = torch.randn(4,10)

    y_pred = model(input)

    print(y_pred.shape)
    print(input)
    print(y_pred)

test1()

torch.Size([4, 5])
tensor([[ 0.4771, 0.7262, 0.0912, -0.3891, 0.5279, 1.0311, -0.7048, 1.0131,
0.7642, 1.0950],
[ 0.3399, 0.7200, 0.4114, -0.5733, 0.5069, -0.4752, -1.1299, -0.1360,
1.6354, 0.6547],
[ 0.5760, -0.3609, -0.0606, 0.0733, 0.4976, -0.4257, -1.3371, -0.1933,
0.6526, -1.9006],
[ 0.2286, 0.0249, 0.1947, -1.6535, 0.6814, 1.4611, -0.3098, -1.6022,
1.3529, 1.2888]])
tensor([[-0.5221, 0.6345, -0.4408, -1.4161, -0.7894],
[-0.3523, 1.0458, -0.2068, -1.1083, -0.2492],
[ 0.3888, -0.0686, -0.2927, -0.1234, 0.3353],
[ 0.2049, 0.3954, 0.5659, -1.4681, -0.4581]],
grad_fn=)

9.1.3 优化器

def test2():
    model = nn.Linear(in_features=10,out_features=5)
    # 传入模型参数和学习率
    optimizer = optim.SGD(model.parameters(),lr=0.01)

    # 此处省略backword

    # 再调用backword之前要梯度清零
    optimizer.zero_grad()
    # 更新模型参数
    optimizer.step()

9.2 数据加载器的使用

9.2.1 数据类创建

如果是引用数据集，那么就自带有这个部分内容

class SampleDataset(Dataset):
    def __init__(self,x,y):
        # 初始化
        self.x = x
        self.y = y
        self.len = len(y)
    def __len__(self):
        # 返回数据总量
        return self.len
    def __getitem__(self, index):
        # 根据索引返回一条样本
        # 将index限定在合理范围内
       index = min(max(index,0),self.len-1)
       return self.x[index],self.y[index]

9.2.2 实例化数据加载类

def test0():
    x = torch.randn(100,8)
    print(x.size())
    y = torch.randint(0,2,(x.size(0),))
    print(y)


    sample_dataset = SampleDataset(x,y)
    print(sample_dataset[0][0])
    print(sample_dataset[0][1])
test0()

torch.Size([100, 8])
tensor([0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1,
0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0,
0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0,
0, 0, 0, 0])
tensor([ 1.1179, -1.2956, 0.0503, -0.5855, -0.3900, 0.0358, 0.1206, -0.8057])
tensor(0)

9.2.3 数据加载类的使用

一次加载多条数据

def test1():
    
    # 构建数据对象
    x = torch.randn(100,8)
    y = torch.randint(0,2,(x.size(0),))
    sample_dataset = SampleDataset(x,y)

    # 使用Dataloader
    dataloader = DataLoader(sample_dataset,
                            batch_size=4,
                            shuffle=True)
    for x,y in dataloader:
        print(x)
        print(y)
        break
    
test1()

tensor([[-0.5414, -1.0563, 0.2413, 0.1828, 0.6247, -0.7940, -0.6748, -0.3877],
[ 0.6420, -0.8497, -0.6987, -0.2052, -0.7812, 0.6873, 0.7836, -1.1109],
[-0.3359, -0.9029, 0.6440, 0.7592, -2.0203, -0.6740, -0.9192, 1.2120],
[-1.2018, -0.5615, -0.9465, -0.7420, 0.1556, -0.2584, -0.7502, 1.2355]])
tensor([0, 0, 0, 0])

9.3 构建简单数据类型

def test2():
    
    # 构建数据对象
    x = torch.randn(100,8)
    y = torch.randint(0,2,(x.size(0),))
    # 使用TensorDataset也可以来构建简单的数据类，就不需要上面的class类了
    sample_dataset = TensorDataset(x,y)
    # 使用Dataloader
    dataloader = DataLoader(sample_dataset,
                            batch_size=4,
                            shuffle=True)
    for x,y in dataloader:
        print(x)
        print(y)
        break
test2()

9.4 使用组件创建线性回归

9.4.1 构建数据集

def create_dataset():
    x, y, coef = make_regression(n_samples=100,
                                 n_features=1,
                                 noise=10,
                                 coef=True,
                                 bias=14.5,
                                 random_state=42)
    # 将构建的数据转换为张量类型
    x = torch.tensor(x, dtype=torch.float32)
    y = torch.tensor(y, dtype=torch.float32).view(-1, 1)  # 转换为列向量
    return x, y, coef

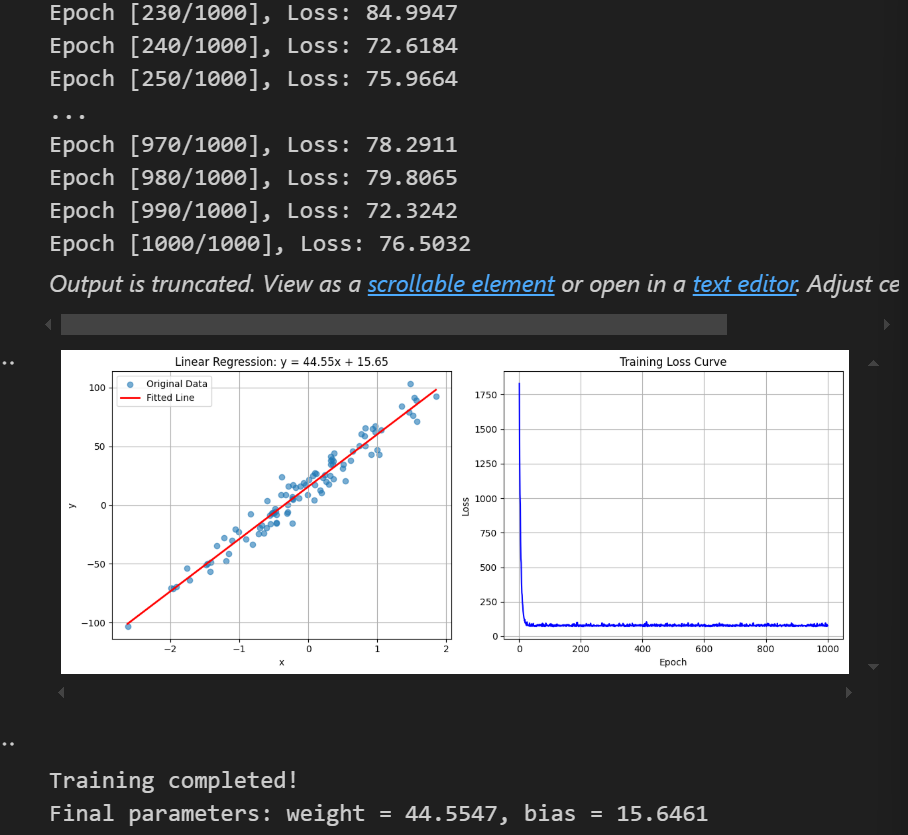
9.4.2 创建训练函数以及训练结果可视化

def train():

    # 创建数据集
    x, y, coef = create_dataset()
    
    # 构建数据对象
    sample_dataset = TensorDataset(x, y)
    # 使用Dataloader
    dataloader = DataLoader(sample_dataset,
                            batch_size=16,
                            shuffle=True)
    
    # 构建线性模型
    model = nn.Linear(in_features=1, out_features=1)
    
    # 构建损失函数
    criterion = nn.MSELoss()
    
    # 优化方法
    optimizer = optim.SGD(model.parameters(), lr=0.01)
    
    # 初始化训练参数
    epochs = 1000
    # 记录每个epoch的损失
    epoch_losses = []
    
    for epoch in range(epochs):
        epoch_loss = 0.0
        batch_count = 0
        
        for train_x, train_y in dataloader:
            # 将一个batch的数据输入模型
            y_pred = model(train_x)
            # 计算损失
            loss = criterion(y_pred, train_y.reshape(-1, 1))
            # 梯度清零
            optimizer.zero_grad()
            # 反向传播
            loss.backward()
            # 更新参数
            optimizer.step()
            
            # 累加损失
            epoch_loss += loss.item()
            batch_count += 1
        
        # 计算平均损失
        avg_loss = epoch_loss / batch_count
        epoch_losses.append(avg_loss)
        
        # 每10个epoch打印一次损失
        if (epoch + 1) % 10 == 0:
            print(f'Epoch [{epoch+1}/{epochs}], Loss: {avg_loss:.4f}')
    
    # ==== 绘制拟合曲线 ====
    plt.figure(figsize=(12, 5))
    
    # 子图1：原始数据和拟合线
    plt.subplot(1, 2, 1)
    # 绘制原始数据点
    plt.scatter(x.numpy(), y.numpy(), alpha=0.6, label='Original Data')
    
    # 生成测试数据用于绘制拟合线
    x_test = torch.linspace(x.min(), x.max(), 100).reshape(-1, 1)
    with torch.no_grad():  # 禁用梯度计算
        y_pred = model(x_test)
    
    # 绘制拟合线
    plt.plot(x_test.numpy(), y_pred.numpy(), 'r-', linewidth=2, label='Fitted Line')
    
    # 获取模型参数
    w, b = model.weight.item(), model.bias.item()
    plt.title(f'Linear Regression: y = {w:.2f}x + {b:.2f}')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.grid(True)
    plt.legend()
    
    # ==== 绘制损失曲线 ====
    plt.subplot(1, 2, 2)
    plt.plot(range(1, epochs + 1), epoch_losses, 'b-')
    plt.title('Training Loss Curve')
    plt.xlabel('Epoch')
    plt.ylabel('Loss')
    plt.grid(True)
    
    plt.tight_layout()
    plt.show()
    
    # 打印最终参数
    print(f'\nTraining completed!')
    print(f'Final parameters: weight = {w:.4f}, bias = {b:.4f}')

# 调用训练函数
train()